How to Find Out if a Point is Inside a Parallelogram

Find if a Point is Inside a Parallelogram

The Code:

function point_in_parallelogram(_point_x,_point_y,_start_x,_start_y,_width,_height,_angle,_NorthEast = true) {
	
	if (point_in_rectangle(_point_x,_point_y,_start_x,_start_y,_start_x+_width,_start_y+_height)) {
	
		var _ratio = dtan(_angle)   // or tan((_angle/360)*(pi*2))
	
		var _pixels_above_top = _point_y - _start_y		// Find how far the mouse is away from the top
		var _side_offset = _pixels_above_top*_ratio		// Side the mouse this amount horizontally
	
		if (!_NorthEast) {_side_offset = (-_side_offset)+(_height*_ratio)} 
		
		return point_in_rectangle(_point_x+_side_offset,_point_y,_start_x+(_height*_ratio),_start_y,_start_x+_width,_start_y+_height)
	
	}
	
}

This function returns true if the point at _point_x and _point_y is inside the parallelogram. It runs very efficiently because it is still checking for a collision with a rectangle (red outline in above image) however it slides the collision point horizontally to match the angle of the parallelogram (black circle).

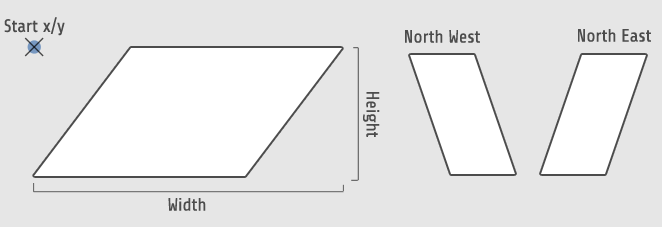
Inputs:

_point_x = The horizontal point you are checking if it collides
_point_y = The vertical point you are checking if it collides
_start_x = This is where the top left of the parallelogram is (See image above)
_start_y = This is where the top left of the parallelogram is (See image above)
_width = The width of the parallelogram (See image above)
_height = The height of the parallelogram (See image above)
_angle = The angle of the parallelogram (See image above)
_NorthEast = Which way is the diagonal angle pointing (to the left or right) (See image above)

Output:

Returns = true/false if the given point is inside the parallelogram

There is one major limit, one of the sides has to be horizontal. Other than that I’m very happy with the speed this runs at and the precision you get.

If you want to get a whole example project you can see it on GitHub: https://github.com/DavidStrachan/GM-point_in_parallelogram

This code could easily be adapted to other languages.